EL SONIDO DEL CAOS

Atem se fundó hace 16 años como un proyecto personal en el que aunar nuestros talentos matemático-artísticos, musicales-pictóricos, con el objetivo fundamental de investigar en inteligencia artificial y el desarrollo de nuevas tecnologías.

Estos últimos años hemos estado trabajando en un proyecto de investigación que hemos denominado Dynasis y que se centra en el estudio y la modelización matemática de sistemas dinámicos. Enmarcado dentro de esta investigación queremos mostraros un espacio experimental que hemos llamado Iripho chaotic Sound.

Iripho Chaotic Sound se podría considerar como un ejemplo de creatividad computacional musical. La utilización de computadoras para crear música, históricamente se ha basado en tomar al músico y su proceso creativo como un referente. Este enfoque ha llevado a desarrollar propuestas, que, por ejemplo, simulan corales al estilo de Bach o a imitar los estilos de compositores como Mozart, Albinoni, Chopin…

El camino que nosotros os vamos a mostrar en esta experiencia es completamente opuesto: se trata de mostraros la creatividad de las máquinas en función de su propia naturaleza.

Antes de contaros la tecnología que hace posible esta experiencia, poneros en el contexto tecnológico, científico y creativo en el que se ha desarrollado.

Entorno Tecnológico:

Desde el punto de vista de la tecnología hemos utilizado una plataforma que denominamos Hyperborea diseñada para crear Sistemas Complejos, que son aquellos en los que interactúan muchos agentes y la combinación de esas interacciones hace difícil de predecir el resultado. 

(ejemplos de Sistemas Complejos: organismos biológicos, ecosistema, un sistema inmunológico o una economía de mercado.)

Hyperborea está dotada de módulos y modelos. los módulos nos permiten procesar y computar millones de datos y los modelos una vez parametrizados en función de esos datos, nos permiten crear soluciones a medida de los retos que se nos planteen. Este proceso de modelización matemática está soportado por la capacidad computacional de la que disponemos, que en el caso de Atem es de aproximadamente 45 teraflops (45 billones de operaciones por segundo)

(el cerebro humano llega a 1 hexaflops que es un trillón de operaciones por segundo.)

(Mientras un supercomputador necesita 21-40 Mw de energía el cerebro humano sólo consume 24w)

Entorno científico: La modelización matemática es posible mediante un proceso de entrenamiento mediante el cual los modelos aprenden de los datos y se adaptan para crear una solución a medida.

Entorno creativo:

Ejemplos: En visión artificial la tecnología actual utiliza la geometría Euclídea para identificar un objeto o a una persona, mientras nosotros utilizamos espacios Topológicos que mediante unos descriptores matemáticos nos definen un objeto o un individuo por aquellos rasgos que le son innatos, aunque se les someta a transformaciones. (gracias a esta tecnología podemos identificar a una persona incluso con el paso del tiempo). 

En lenguaje natural utilizamos vectores matemáticos en lugar de palabras para evitar la ambigüedad del lenguaje. 

Finalmente, en cuanto a la capacidad de componer música hemos dotado a las máquinas de un proceso mediante el cual hemos creado redes neuronales que simulan el caos y que generan su propio espacio sonoro-musical.

En la vida cotidiana, solemos utilizar términos como caos, caótico como sinónimos de confuso, desordenado, descontrolado…pero según la teoría del caos, que es la rama matemática que estudia el caos, ¿es realmente el caos algo confuso, desordenado o descontrolado? ¿cuál es la definición precisa de caos? ¿se puede representar el caos gráficamente? ¿se puede representar el caos mediante el sonido? Para responder a estas preguntas nos ayudaremos de lo que entendemos como sistemas dinámicos. Pero ¿qué es un sistema dinámico? Un sistema es un ente u objeto que está compuesto de diferentes componentes o partes que se interrelacionan de alguna manera entre sí.  Los sistemas dinámicos son aquellos en los que su comportamiento cambia o evoluciona con el paso del tiempo. Dentro de los sistemas dinámicos tenemos aquellos que varían de manera continua en el tiempo, como el movimiento de un péndulo. Por contra, también existen sistemas dinámicos que varían de manera discreta o a saltos como las funciones iterativas que son muy interesantes para el estudio del caos.

Una función iterativa es un sistema dinámico discreto donde la salida del sistema actual se utiliza como entrada del sistema en el instante siguiente, es decir el sistema es retroalimentado. 

(Ejemplo retroalimentamos el sistema con el cuadrado de un número. Si escogemos un valor inicial o semilla de 2 y lo introducimos en el sistema, este nos devuelve 4 que al reintroducirlo de nuevo en el sistema, nos devolvería 16 y asi sucesivamente.)

Esto nos lleva a la secuencia de números en el tiempo que es denominada la órbita del sistema dinámico. Vemos que la órbita de este ejemplo tiende hacerse cada vez más grande y no está acotada, por lo que en este caso diremos que la orbita diverge.

Dentro de las funciones iterativas, la ecuación logística o función logística es especialmente interesante para el estudio del caos. Se suele utilizar en modelos de crecimiento de poblaciones y propagación de enfermedades entre otras cosas. 

En edta función si variamos el parámetro “r “, a valores cada vez más grandes, el comportamiento en el tiempo del sistema dinámico va cambiando radicalmente. 

(Por ejemplo, con r=2 y un valor inicial de 0.71 la órbita del sistema se estabiliza en el punto fijo 0.5 y ya no cambia más. Lo mismo ocurre con un valor inicial de 0.91. De hecho, cualquier valor inicial o semilla acaba estabilizándose en el punto fijo 0.5 cuando r es igual a 2. Por lo tanto, diremos que el punto fijo 0.5 es un atractor del sistema dinámico cuando r es igual a 2).

Cuando r es igual a 3.2, el comportamiento cambia, y el sistema después de unas pocas iteraciones acaba oscilando periódicamente entre dos valores. Por ello diremos que es sistema tiene una órbita periódica, y en este caso de orden 2 porque oscila entre 2 valores. Está orbita periódica también denominada ciclo limite, también es un atractor como en el caso del punto fijo, ya que cualquier valor inicial que escojamos acaba orbitando cíclicamente entre estos dos valores después de unas pocas iteraciones. Cuando r es igual a 3.52 el sistema se ve atraído por un ciclo límite de orden 4, oscila entre 4 valores. De hecho, a medida que r se va acercando a 4, el sistema dinámico se ve atraído por ciclos límites de orden cada vez más grande.

Pero la sorpresa llega cuando r está muy cerca de 4. Con r igual a 3.99 y un valor inicial de 0.71, el sistema no es atraído por ningún ciclo límite ni punto fijo. Orbita de manera aperiódica, podríamos pensar que aleatoriamente, lo cual como veremos posteriormente no es cierto. Además, la órbita del sistema siempre esta acotada entre 0 y 1 no crece ni decrece de manera ilimitada. 

Otra curiosidad es, que si cogemos un valor inicial muy muy cercano a nuestro primer valor inicial 0.71 como por ejemplo 0.711 podríamos pensar que sus orbitas deberían ser muy similares, pero los sorprendente es que en apenas 6 iteraciones,  las orbitas se comienzan a separar dramáticamente, estando en puntos prácticamente contrarios en la iteración 14. Cuando pequeños cambios en las condiciones iniciales conducen a variaciones radicales en la órbita de un sistema dinámico diremos que el sistema dinámico es sensible a las condiciones iniciales. Con todo esto, tenemos ya todo lo que necesitamos para definir el caos de manera precisa.

Diremos que un sistema dinámico es caótico si posee las siguientes propiedades: 

• Está regido por una regla determinista, como en nuestro ejemplo por una ecuación, donde utilizando la misma entrada siempre obtenemos la misma salida, a diferencia de modelos no deterministas como por ejemplo el resultado del lanzamiento de una moneda donde no tenemos la certidumbre del resultado, de si será cara o cruz. 

• Otra propiedad es que la órbita del sistema sea aperiódica y además acotada. 

• Por último, el sistema debe tener alta sensibilidad a las condiciones iniciales. 

Por lo tanto, la ecuación logística con r igual a 3.99 cumple todas las propiedades por lo que es un sistema dinámico caótico.

Ya hemos visto anteriormente que los sistemas dinámicos no caóticos podían tener atractores como los puntos fijos o los ciclos límites. Pero los sistemas dinámicos caóticos también tienen su atractor denominado atractor extraño o atractor caótico. 

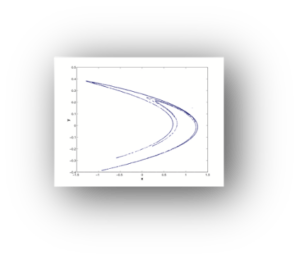Por ejemplo, un sistema dinámico caótico discreto, como el llamado mapa de Henon, a diferencia de la ecuación logística, devuelve 2 valores en cada iteración en lugar de 1. Podemos utilizar estos 2 valores como coordenadas x e y para dibujar el sistema dinámico caótico en el plano. Sorprendentemente el plano no se llena completamente de puntos como ocurriría si graficáramos algo completamente aleatorio, sino que los puntos caen siempre dentro de este dibujo en cada una de las iteraciones. 

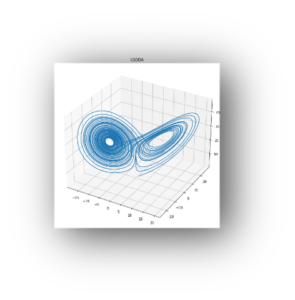
No podemos predecir exactamente en qué parte del dibujo se dibujará la siguiente iteración pero lo que sí sabemos es que nunca se dibujará fuera del dibujo. Este dibujo es el atractor caótico del mapa de Henon y demuestra que el caos tiene una estructura y unas reglas. Este otro gráfico de aquí es el atractor de Lorenz, correspondiente a un sistema dinámico caótico continuo utilizado para modelizar la atmosfera terrestre. Devuelve 3 valores en lugar de dos por lo que los podemos graficar en un espacio tridimensional. Como vemos, tiene una estructura muy curiosa.

Por lo tanto, hemos visto que es posible representar gráficamente el caos, y en Atem Nuevas Tecnologías hemos ideado un procedimiento para representar el caos, concretamente un atractor caótico, como sonido.  Para ello, hemos simulado un sistema dinámico caótico con un computador mediante redes neuronales artificiales. Las redes neuronales artificiales simulan el funcionamiento de las redes neuronales biológicas y son utilizadas en el mundo de la inteligencia artificial para muchos propósitos como visión artificial, creación de modelos predictivos, etc.

Hemos modificado las redes neuronales estándar para añadirlas un comportamiento caótico y puedan ser retroalimentadas. Para este proyecto hemos usado una red neuronal con esta estructura. Como vemos tiene 4 neuronas de entrada, 2 en la capa intermedia que añaden el comportamiento caótico y 4 neuronas de salida, las flechas indican que la red está retroalimentada. Al tener 4 neuronas de salida la red devolverá 4 valores que utilizaremos para modelizar el sonido. Estos 4 valores se pueden interpretar como las coordenadas de un punto del atractor caótico de 4 dimensiones generado por la red neuronal caótica, y cada iteración ira recorriendo distintos puntos del atractor convirtiéndolos en sonido.

Utilizaremos un sintetizador analógico modular Moog como generador del sonido. Moog fue el primer sintetizador comercial de la historia y su sonido es una leyenda de la música.

El procedimiento para la creación del sonido es el siguiente:

Los 4 valores devueltos por la red neuronal en cada iteración son convertidos en voltaje y enviados al sintetizador. 

• El primer valor determinará el voltaje que se ha de suministrar a los osciladores del sintetizador y estos reproducirán un tono o nota. 

• El segundo determina el voltaje suministrado al amplificador del sintetizador, lo cual afectara a la amplitud del sonido.  

• El tercero determina el voltaje suministrado a la modulación del corte del filtro del sintetizador el cual determinará el timbre del sonido. 

• Y el cuarto determina el voltaje suministrado a la modulación del ataque de la envolvente del sintetizador el cual determinará la duración del sonido. 

• Por último, el reloj del sintetizador determina cuando se debe retroalimentar la red neuronal para generar un sonido nuevo.

Es importante destacar que todo esto se genera en tiempo real por lo que el sintetizador puede generar sonido de manera ilimitada recorriendo el atractor caótico una y otra vez. Veremos que, aunque es imposible predecir que sonido se generará en la siguiente iteración y no hay ningún patrón claro, si subyace una estructura común y el resultado desde nuestro punto de vista es más musical de lo que cabría esperar. Juzguen ustedes.